Intellectual activism in defense of the American way of life.
Archive for December, 2002
No Gore in ’04
Dec 15th
It seems that Al Gore won’t run in ’04 after all, clearing the way for (the marginally better candidates) Tom Daschle, Dick Gephardt, and Lieberman. Either way, as long as the Dems fail to get their act together and find something to stand for, Bush’s re-election should be a shoe-in.
Also, while advertising the upcoming speech on Abortion, I started a lively (perhaps too lively) debate on TexAgs.com which is probably the most active thread ever outside their college football section.
Quoth one commie
Dec 14th
“We need [Moore's] noisy, cocky energy, his passion and class consciousness; we need his shticks, we need his stones.”
Anyone who wants more proof that Hollywood/media is commie heaven should note the
13 positive and 0 negative reviews on Michael Moore’s latest manifesto: Bowling for Columbine.
Oops!
Dec 13th
I overclocked my computer a few days ago, disabling its ability to reboot. Last night, it rebooted to apply an automatic update, but becuase of the overclock, it didn’t come back up, and after a few hours, Cox reset my IP address, causing the DNS entry to be erroneous. So, my website will be down for a day or two, until the new DNS clears…
Random clips from the news…
Dec 12th
Ted Turner on terrorism: “There’s a lot of despair out there. Despair and poverty… these breed anger. And, I think, that’s one of the reasons terrorism exists. There’s so much frustration, anger, and despair..In the Arab view, America doesn’t do enough to help them and that’s why they’re so angry at it,” he said. The battle against terrorism is a battle against poverty and injustice. People are willing to die when they don’t have anything to live for.”
meanwhile, “poverty-stricken …. North Korea’s Foreign Ministry said Thursday it would immediately end a freeze on its nuclear power plant in response to an allied decision to suspend oil aid to Pyongyang,.Under a 1994 pact, Pyongyang promised to scrap plans to develop nuclear weapons in return for light water nuclear reactors and fuel oil supplies.”
as, US forced seized then released an unmarked, North Korean freighter loaded with Scuds and chemicals:
“The real name of the North Korean ship had been painted over, so too had the registration number. The vessel was not flying a flag which Señor Trillo said meant the Spanish crew was within its legal rights to seize the vessel.At first the So San’s captain claimed she was a Cambodian vessel but on seeing marines clambering into launches and heading in his direction he asked if he could contact his masters in Pyongyang. “
“Señor Trillo listed the haul as 15 Scud missiles, 15 conventional warheads, 23 tanks of nitric acid rocket propellant and 85 drums of chemicals.”
The ship was allowed to go on with all it’s cargo after “The [Yemeni] Sanaa Government insisted the Scuds were for their own defence and were indignant at suggestions the missiles could fall into unscrupulous hands.”
Also, apparently Palestinian rule seems to have it’s flaws:
“Crime wave in West Bank as unpaid cops turn rogue…A network of gangs have appeared that extort from businessmen, steal property and other assets and work for those who want to eliminate their rivals. The sources said the gangs operate in the Jerusalem and Ramallah areas and face virtually no danger from being captured by either Israeli or Palestinian authorities.”
Let’s see if they can dig themselves out of this hole
Dec 10th
Gray Davis and the California democrats have done it again: California is on the edge of bankruptcy. Apparently all those “progressive” social programs couldn’t survive the recession.
Personally, I’m glad. Those stupid democrats have dug themselves into this hole, and I hope they feel the pain on the way out. After all, CA is unionized to hell, and they will have to convince all those teachers and state workers to take massive pay cuts /lay offs.
Either that, or raise taxes. But higher taxes will scare away even more business, digging them into an even bigger hole. Either way, California is screwed. Apparently, the highly progressive tax system in CA had a part to play:
“California prides itself on its progressive income tax, with people earning high incomes paying a huge share of state taxes. The top 10 percent of filers pay 75 percent of personal income taxes. But when their income drops, as it did when the technology boom went bust in early 2000, the state treasury crashes.”
It seems that you can’t milk the rich for all the’re worth after all. The Dems are still clueless though:
“Mr. Wesson, the Assembly speaker, said it was “mathematically impossible” to balance the state budget without raising taxes.
“The way you do it is to put absolutely everything on the table, every conceivable cut, every conceivable way to raise taxes,” he said. “Then you sort out what is the least painful and what is the most fair.”
The likely outcome, I think, is that taxes will go up, and many of California’s businesses will go away. NYC’s tax hike had (and will have) much the same effect. I’m hopeful that NYC and CA will learn a lesson from this, but somehow, I doubt it. Nevertheless, the lesson is not lost on all, as thisUSA Today story from a while back shows
The Relationship Between Economic Freedom and Prosperity Around The World
Dec 10th
Econometrics 463 Term Project:
The Relationship Between
Economic Freedom and Prosperity Around The World
By David V.
December 10, 2002
Introduction
The collapse of the Soviet Union has been followed by worldwide economic liberalization and increasing international trade. The increase in economic freedom has been followed by a global increase in prosperity, but not without setbacks. The economic slowdown beginning in the late 1990’s has caused some to question the progress of economic liberalization as well as its benefits. An analysis of relationship between economic freedom and prosperity may be useful in determining whether economic freedom increases prosperity and which specific factors have the greatest effect on wealth. This information would be very useful to anyone seeking to determine the weakness of various governmental policies. Governments may find it important to know which factors have the greatest effect on economic growth and investors may find it helpful to predict which countries are more likely to develop as potential markets.
Methodology
For this paper, ten factors that measure different aspects of economic freedom were correlated against the 2001 per capita GDP of 155 nations. There have been several studies on economic freedom since 1980 (Easton, 1997) by various think tanks. The Heritage Institute results were used for this paper because they measured the largest number of factors, and had data for over 155 countries –more than the other studies. For the GDP data, the 2001 results from the CIA Factbook were used because the CIA had the most complete and generally the latest GDP data. The Heritage Institute’s 2003 report actually came out in November 2002, but the 2001 data was used because for the majority of countries, the latest available GDP data is still for 2000 or 2001. A comparison of the Heritage Institute evaluations of economic freedom to those of the Fraser Institute (2002), showed that the reports all gave the same approximate evaluations of economic freedom.
There were ten independent variables tested: (the abbreviations used in are parenthesis)
• Trade policy (Trade)
• Fiscal burden of government (FiscalBu)
• Government intervention in the economy (Governme)
• Monetary policy (Monetary)
• Capital flows and foreign investment (ForeignI)
• Banking and finance (BK)
• Wages and prices (Wagesand)
• Property rights (Property)
• Regulation (RG)
• Black market (BlackMar)
Each of these variables was a cardinal value from one to five, with one being the least government involvement and five being the most. The dependent variable was indGDP, the 2001 per capita GDP. Additional variables considered were Econ_Sco, the overall economic score and WorldRan, the ranking according to the overall score.
Regressions were run on the overall economic score and then the ten independent variable. Initially a linear model was used, then all the variables were tested for significance under logarithmic, quadratic, and interactive relations, and variables that were not significant under any test at the 5% level were dropped from the model.
The CIA data had estimated GDP data for 236 regions — almost every country and territory on earth, but the Heritage listed 161 countries. Of these, 155 had data available for all ten variables, so 155 countries and 10 factors were used in estimating the model. The software used for all the regressions was Gretl.
Procedure
The first step was to find out what overall relationships were present in the model. For this regression, the indGDP and Econ_Sco variables were used. A linear regression between them produced an unadjusted R-squared of 0.496862.
VARIABLE COEFFICIENT STDERROR T STAT 2Prob(t > |T|)
0) const 34622.6 2160.89 16.022 < 0.00001 ***
5) Econ_Sco -8480.91 689.958 -12.292 < 0.00001 ***
Mean of dependent variable = 8854.32
Standard deviation of dep. var. = 9169.89
Sum of squared residuals = 6.51533e+009
Standard error of residuals = 6525.63
Unadjusted R-squared = 0.496862
Adjusted R-squared = 0.493573
A more closer match was found by adding sq_Econ to the model:
VARIABLE COEFFICIENT STDERROR T STAT 2Prob(t > |T|)
0) const 76270.6 5767.89 13.223 < 0.00001 ***
5) Econ_Sco -36958.0 3782.94 -9.770 < 0.00001 ***
17) sq_Econ_ 4575.07 600.351 7.621 < 0.00001 ***
Mean of dependent variable = 8854.32
Standard deviation of dep. var. = 9169.89
Sum of squared residuals = 4.71419e+009
Standard error of residuals = 5569.06
Unadjusted R-squared = 0.635953
Adjusted R-squared = 0.631163
The graph below shows the predicted model and the Econ_Sco variables:
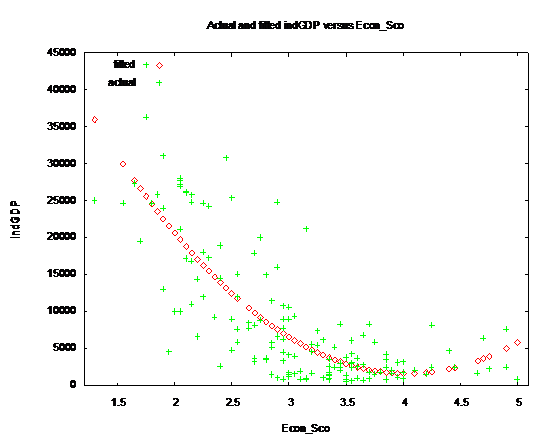
The relationship here is clear: increasing government involvement lowers GDP at a rate of $36, 958 per index point. The quadratic function seems to indicate that super-high levels of involvement actually raise GDP, but only about six countries seem to be part of that trend, with two having a per capita GDP above 5000: Iran and Libya.
After a simple one-factor regression, a regression with all ten factors (but not Econ_Sco) was attempted. Initially, a simple linear regression was used with all 155 variables and all 10 factors, without any quadratic or interacting variables:
VARIABLE COEFFICIENT STDERROR T STAT 2Prob(t > |T|)
0) const 20847.5 2372.98 8.785 < 0.00001 ***
6) Trade -1209.12 445.846 -2.712 0.007503 ***
7) FiscalBu 1576.36 481.540 3.274 0.001330 ***
![]() Governme 976.563 594.194 1.644 0.102459
Governme 976.563 594.194 1.644 0.102459
9) Monetary -609.650 333.642 -1.827 0.069732 *
10) ForeignI 194.577 720.675 0.270 0.787553
11) BK -826.296 689.728 -1.198 0.232884
12) Wagesand 1382.06 720.518 1.918 0.057071 *
13) Property -2068.62 739.690 -2.797 0.005870 ***
14) RG -213.362 838.028 -0.255 0.799395
15) BlackMar -2863.18 535.661 -5.345 < 0.00001 ***
Mean of dependent variable = 8854.32
Standard deviation of dep. var. = 9169.89
Sum of squared residuals = 3.43621e+009
Standard error of residuals = 4884.93
Unadjusted R-squared = 0.734643
Adjusted R-squared = 0.716216
F-statistic (10, 144) = 39.8665 (p-value < 0.00001)
Durbin-Watson statistic = 2.14011
First-order autocorrelation coeff. = -0.071209
(Higher coefficients indicate higher government involvement in the various areas.)
A test for quadratic variables was used:
VARIABLE COEFFICIENT STDERROR T STAT 2Prob(t > |T|)
0) const 25616.2 5818.15 4.403 0.000022 ***
6) Trade 3241.39 1794.43 1.806 0.073105 *
7) FiscalBu -4843.72 2560.55 -1.892 0.060693 *
![]() Governme 596.296 2228.13 0.268 0.789402
Governme 596.296 2228.13 0.268 0.789402
9) Monetary -263.771 1262.99 -0.209 0.834885
10) ForeignI -867.630 2083.24 -0.416 0.677725
11) BK -2086.66 1858.50 -1.123 0.263547
12) Wagesand -2955.80 2517.71 -1.174 0.242476
13) Property -3070.39 1991.59 -1.542 0.125510
14) RG -1281.77 2795.31 -0.459 0.647305
15) BlackMar -7242.81 1796.90 -4.031 0.000093 ***
16) sq_Trade -423.008 265.461 -1.593 0.113407
17) sq_Fisca 744.970 378.890 1.966 0.051343 *
18) sq_Gover -149.109 386.857 -0.385 0.700524
19) sq_Monet 121.290 207.138 0.586 0.559160
20) sq_Forei 88.0300 369.384 0.238 0.812000
21) sq_BK 338.051 314.633 1.074 0.284561
22) sq_Wages 216.479 414.127 0.523 0.602022
23) sq_Prope 626.785 334.349 1.875 0.063019 *
24) sq_RG 135.053 428.646 0.315 0.753199
25) sq_Black 1210.16 262.880 4.603 < 0.00001 ***
Unadjusted R-squared = 0.396284
Adjusted R-squared = 0.306177
Test statistic: TR^2 = 61.424005,
with p-value = prob(Chi-square(10) > 61.424005) = 0.000000
And a test for logs:
VARIABLE COEFFICIENT STDERROR T STAT 2Prob(t > |T|)
0) const -1873.56 2260.44 -0.829 0.408665
6) Trade -1990.24 1334.03 -1.492 0.138075
7) FiscalBu 4059.26 2287.05 1.775 0.078187 *
![]() Governme -506.908 1945.41 -0.261 0.794827
Governme -506.908 1945.41 -0.261 0.794827
9) Monetary 804.378 1058.59 0.760 0.448676
10) ForeignI 192.145 1865.56 0.103 0.918120
11) BK 1984.84 1670.56 1.188 0.236883
12) Wagesand 847.905 2099.09 0.404 0.686902
13) Property 3116.16 1779.32 1.751 0.082179 *
14) RG 343.683 2304.40 0.149 0.881666
15) BlackMar 6442.66 1340.24 4.807 < 0.00001 ***
17) l_Trade 6925.99 3734.78 1.854 0.065872 *
18) l_Fiscal -12569.4 7106.97 -1.769 0.079236 *
19) l_Govern 978.852 4892.75 0.200 0.841736
20) l_Moneta -960.438 2574.34 -0.373 0.709678
21) l_Foreig -1249.52 4273.17 -0.292 0.770425
22) l_BK -4921.49 3858.68 -1.275 0.204362
23) l_Wagesa -6570.98 5447.23 -1.206 0.229828
24) l_Proper -6491.89 4115.55 -1.577 0.117061
25) l_RG -2554.60 6290.98 -0.406 0.685337
26) l_BlackM -16450.3 3732.15 -4.408 0.000021 ***
Unadjusted R-squared = 0.411176
Adjusted R-squared = 0.323292
Test statistic: TR^2 = 63.732241,
with p-value = prob(Chi-square(10) > 63.732241) = 0.000000
It appears that sq_Fisca, sq_Prope, sq_Black, and l_Trade and l_BlackM are significant, so these variables were created:
Model 2: OLS estimates using the 155 observations 1-155
Dependent variable: indGDP
VARIABLE COEFFICIENT STDERROR T STAT 2Prob(t > |T|)
0) const 34351.3 9683.62 3.547 0.000531 ***
6) Trade -2750.11 1190.66 -2.310 0.022376 **
7) FiscalBu -2757.13 2424.35 -1.137 0.257385
![]() Governme 964.732 488.511 1.975 0.050267 *
Governme 964.732 488.511 1.975 0.050267 *
9) Monetary -109.990 271.083 -0.406 0.685555
10) ForeignI -190.634 582.886 -0.327 0.744120
11) BK -965.605 556.143 -1.736 0.084735 *
12) Wagesand -63.7690 603.954 -0.106 0.916063
13) Property -5953.28 1787.79 -3.330 0.001112 ***
14) RG -867.724 679.755 -1.277 0.203899
15) BlackMar 1615.02 9421.44 0.171 0.864143
16) l_Trade 5907.95 3327.77 1.775 0.078029 *
17) l_BlackM -15172.6 11337.6 -1.338 0.182998
18) sq_Fisca 651.370 362.476 1.797 0.074507 *
19) sq_Prope 800.209 284.262 2.815 0.005586 ***
20) sq_Black 233.137 848.323 0.275 0.783861
Mean of dependent variable = 8854.32
Standard deviation of dep. var. = 9169.89
Sum of squared residuals = 2.08499e+009
Standard error of residuals = 3872.98
Unadjusted R-squared = 0.838989
Adjusted R-squared = 0.821614
F-statistic (15, 139) = 48.2863 (p-value < 0.00001)
Durbin-Watson statistic = 1.84585
First-order autocorrelation coeff. = 0.0767549
Taking out the non-significant variables, the resulting regression is:
Model 3: OLS estimates using the 155 observations 1-155
Dependent variable: indGDP
VARIABLE COEFFICIENT STDERROR T STAT 2Prob(t > |T|)
0) const 31596.2 2336.61 13.522 < 0.00001 ***
6) Trade -2970.81 1199.32 -2.477 0.014387 **
![]() Governme 756.926 481.722 1.571 0.118279
Governme 756.926 481.722 1.571 0.118279
11) BK -1047.66 493.696 -2.122 0.035519 **
13) Property -8954.56 1615.13 -5.544 < 0.00001 ***
16) l_Trade 6379.73 3351.79 1.903 0.058959 *
17) l_BlackM -7828.71 1176.19 -6.656 < 0.00001 ***
18) sq_Fisca 242.486 56.5346 4.289 0.000032 ***
19) sq_Prope 1273.94 249.607 5.104 < 0.00001 ***
Mean of dependent variable = 8854.32
Standard deviation of dep. var. = 9169.89
Sum of squared residuals = 2.3127e+009
Standard error of residuals = 3980
Unadjusted R-squared = 0.821405
Adjusted R-squared = 0.811619
F-statistic (8, 146) = 83.9364 (p-value < 0.00001)
Durbin-Watson statistic = 1.97101
First-order autocorrelation coeff. = 0.0129411
Government and log(Trade) do not appear to be significant in this model, so they were dropped:
VARIABLE COEFFICIENT STDERROR T STAT 2Prob(t > |T|)
0) const 32948.4 2093.65 15.737 < 0.00001 ***
6) Trade -701.47 352.948 -1.987 0.048715 **
11) BK -930.70 492.710 -1.889 0.060856 *
13) Property -9310.0 1571.14 -5.926 < 0.00001 ***
18) l_BlackM -7606.7 1174.58 -6.476 < 0.00001 ***
19) sq_Fisca 255.859 56.3419 4.541 0.000012 ***
20) sq_Prope 1329.27 242.992 5.470 < 0.00001 ***
Mean of dependent variable = 8854.32
Standard deviation of dep. var. = 9169.89
Sum of squared residuals = 2.40055e+009
Standard error of residuals = 4027.4
Unadjusted R-squared = 0.814621
Adjusted R-squared = 0.807105
F-statistic (6, 148) = 108.394 (p-value < 0.00001)
Durbin-Watson statistic = 2.01359
First-order autocorrelation coeff. = -0.00986223
The estimated model was thus:
indGDP=32948.4 -701.47 *Trade -930.70 BK–9310.0 *Property-7606.7 *log(BlackM)+ 255.859 *Fiscal^2 + 1329.27 *Property^2
(The mean of indGDP was 8854.323 and S.D. was 9169.893 , and the mean of Econ_Sco was 3.0384 and S.D. of 0.76215.)
Below are the observed versus fitted ingGDP residuals:
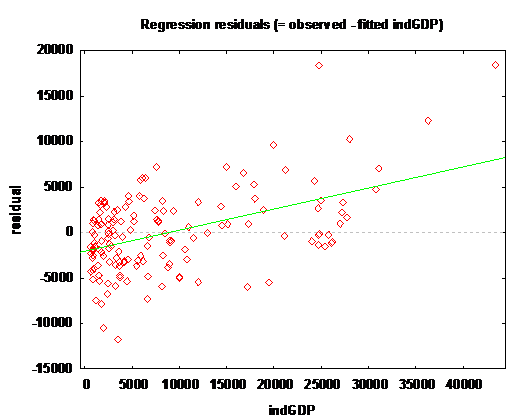
Summary and Discussion
The most obvious evidence shown by the data is that the average value of economic freedom has a strong relationship with per capita GDP. The R-squared value in the quadratic model with Econ_Sco is 0.635953 and at least up to a freedom factor of about 4.2, where the trend suddenly reverses. This may be because the three outliers at the 4.5 range (Libya (capita GDP of 7600) Iran (capita GDP of 6400), and Iraq (capita GDP of 2500)) are socialist economies that maintain unusually high incomes because they derive most of their GDP from oil exports. However, the quadratic relation also suggests that increasing government involvement is progressively less harmful to indGDP. On the other hand, this also means that decreasing government involvement is exponetial more beneficial to GDP.
The final model derived from the regressions was:
indGDP=32948.4 -701.47 *Trade -930.70 BK–9310.0 *Property-7606.7 *log(BlackM)+ 255.859 *Fiscal^2 + 1329.27 *Property^2
This model has several interesting properties. First, it is surprisingly accurate at predicting per capita GDP. With an R-squared of 0.814621, it indicates that 81 percent of variation in wealth between countries is caused by their economic policies. This makes the fact that increased economic freedom leads to more prosperity is hard to dispute. The model also shows that other than the small positive coefficient on fiscal burden, there are strong negative correlations between the above factors and prosperity: that is, free trade, strong property rights, and low black market activity lead to higher prosperity. The question of what exact effect the factors had on GDP and which factors were most influences was more complicated however.
The BlackM factor, or the amount of black market activity shows a high negative, suggesting that the more market activity is conducted underground, the lower the level of GDP. This is highly intuitive, as illegal and hidden activities are bound to have significantly higher costs because of the usual costs risk associated with operating against the law. These factors may be a good proxy for how difficult it is to run a business legally in any given country. Of course when a large percentage of business is underground, most of the legal restrictions on businesses do not apply, which may diminish the accuracy of the other variables at high levels of black market activity. There are 45 countries with the highest level of black market activities, with an average economic freedom ranking of about 124, and average capita GDP of $2,746, significantly below the world average of $8,854.
Trade was another major factor. The quadratic relationship suggests that increasing free trade yields diminishing returns, but the overall pattern was clear: the 34 nations with the highest level of trade restrictions have a capita GDP of $3,578.53 and the top eight nations with the highest level of trade freedom have an average capita GDP of $11,577.5. Since the grading system uses cardinal rather than quantitative rankings, it was hard to get more precise estimates of the effect of trade restrictions, but free trade nevertheless seems to be an important factor for GDP growth. Economic theory would suggest this outcome, since foreign investment is key in the growth of developing nations. A time series study on the growth in GDP versus trade restrictions may clarify this theory.
Property rights had the biggest coefficient out of all the other factors, which is not at all surprising, considering that private property ownership is at the root of capitalism. However the relationship was not linear, as the plot of the actual and fitted indGDP versus Property bellow shows:
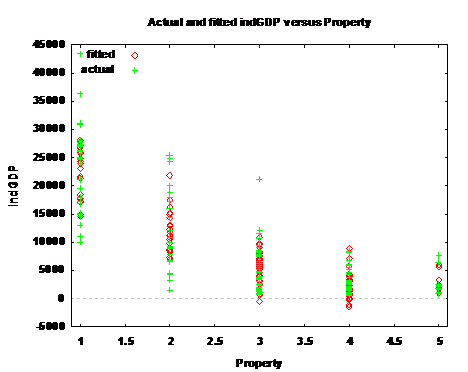
Despite the non-linear relationship, the trend in the quadratic relationship reverses itself only in unfree countries, which may be an indication that property rights are less effective in nations that already have weak property rights protections. Indeed, the average per capita income in the 14 nations with the lowest level of property rights is $2,563.08 and their average ranking is only 144.6 out of 155.
An unexpected result of the model was that increasing fiscal burden (which is defined as “tax rates and the level of government expenditures” (Heritage p53)) seems to actually raise per capita GDP. This may be explained by the fact that as nations get wealthier, increasing profits allow higher taxes to be raised. Nevertheless, taxes do not seem to have a significant impact on GDP, and are probably not the first thing a country should look to cut if it desires economic growth
It is unclear why a number of variables (like foreign investment) that are clearly significant individually were not significant in the full model. When a regression was done on the individual variables, nearly all (other than fiscal burden) variables show significant negative correlations between more government and per capita GDP. This suggests that there is some degree of collinearity in the variables, which is not surprising considering that each factor attempts to isolate certain aspects of bureaucratic policy from a single structure of regulation.
While the particular relationship between the ten factors used is less than clear, the basic conclusion from the data is beyond question: increasing levels of economic freedom are highly correlated with increasing levels of per capita GDP, and the variation in economic freedom explains most of the differences in wealth around the world. This outcome would be surprising to many individuals who attribute factors like natural resources, population growth, or income distributions to differences in wealth, and holds many lessons for anyone attempting to stimulate growth in their own country or companies looking for growth opportunities around the world.
References
1. Easton, S. T., and Walker, M.A., eds. (1992) Rating Global Economic Freedom. Vancouver, B.C., Canada: The Fraser Institute.
2. Hanke, S.H., and Walters, S.J.K. (1997) Liberty, Equality, Prosperity. A Report to the Senate Joint Economic Committee. Washington, D.C.: U.S. Senate.
3. Gerald P. O’Driscoll, Jr., Kim R. Holmes, (2002) 2002 Index of Economic Freedom. Washington, D.C.: The Heritage Foundation.
3. Gerald P. O’Driscoll, Jr., Edwin J. Feulner, (2002) 2003 Index of Economic Freedom. Washington, D.C.: The Heritage Foundation.
4. CIA World Factbook 2002.
http://www.cia.gov/cia/publications/factbook/
5. Economic Freedom of the World, 2000. (2002) Fraser Institute.
http://www.freetheworld.com
6. Gwartney, James, and Lawson, Robert. Capital University Economic Freedom of the World Annual Report 2002: Cato Institute.
http://www.cato.org/economicfreedom
Google, Censorship, and the Hostage Dilemma
Dec 9th
Google, Censorship, and the Hostage Dilemma
David V.
December 9, 2002
On September 8, 2002, the Chinese government blocked Google, one of the Internet’s biggest search engines. The government of China regularly blocks websites that it considers “dangerous” to its regime, but Google.com is a search engine – it only indexes the Internet without bias or preference to the content of a particular website. So why would Google be banned in China, especially considering that it is a crucial research tool without adequate Chinese substitutes? I believe that the answer lies in a game theory scenario known as the hostage dilemma. Because Google had the potential to greatly improve coordination between pro-democracy supporters, it may pose a threat to the Chinese regime. While the exact intentions of China in blocking Google are not clear, the incident holds a lesson for anyone trying to support or suppress democratic movements in authoritarian regimes.
It has been widely recognized that preventing communication and coordination is key to suppressing dissent in an authoritarian regime. Governments have a much easier time subjugating their citizens when there are no organizations through which one may express dissent. Louis XVI failed to learn this lesson when he called together the Estates General to raise money and ended up being beheaded when the delegates teamed up against him. Gorbachev may have forgotten it as well, as his policy of glasnost not only exposed the Soviet Union to the west, but allowed the democratic movement to organize the a government, leading to the collapse of the USSR. In China and Cuba, dissidents are severely punished and isolated from their peers, for any statements that paint the state in a bad light. It is clear that authoritarian regimes not only have an interest in suppressing opposition, but preventing coordination among dissidents as well.
Traditionally, opposition groups have used conventional means of communications to coordinate their efforts, but in an oppressive (and especially urban) society, this poses many problems. In person communication requires planning, which may be intercepted by the government. Telephone calls, mail, and print publications can be recorded or seized and the organizers arrested. While local interpersonal communication is hard to trace, any organization on a national level is nearly impossible to organize in an authoritarian regime because of the hazards to the organizers. Many of these regimes are almost universally opposed by their citizens, but because a coordinated revolt is very difficult to organize, oppressive regimes may persist for many years.
However, governments cannot keep an eye on every citizen, and therefore they must find a way to set up incentives so that no citizen would want to engage in “counter-revolutionary” activities, even if the risk of getting caught is small. Many methods have been devised to do this over they years. The most obvious is to impose severe punishments for even minor infractions, so that the high cost of protest makes opposition too risky for most. Another common method is to refuse to distinguish political dissidents from common criminals, thereby denying dissidents the possibility of martyrdom. Penetrating social structure is yet another method – for example, breaking of weakening familial bonds by raising children away from parents and encouraging them to turn in any critics of government, even family members. A similar strategy is to replace old social organizations with new party-oriented ones, and set up leadership arrangements so that the most loyal party members are always in charge. For example, in China, the State runs labor organizations, youth leagues, and otherwise maintains a monopoly on all organizations, so that no non-governmental framework exists to organize dissent. Perhaps this is why China so opposed to Falun Gong – it represents an entity outside of its control, unlike the government authorized and controlled Catholic and Buddhist churches/temples.
The growth of the Internet poses a significant threat to authoritarian an government’s ability to monitor its citizens. The Internet allows communication to be instant, relatively anonymous, globally accessible, and perhaps most damaging of all, it allows citizens to learn about living standards and political philosophies of free nations. For this reason, most authoritarian regimes have restricted Internet access to varying degrees. In Cuba, where only a tiny minority of the population can even afford a computer, domestic Internet access is still banned. Citizens may only access email for a steep fee in government Post Offices, and nowhere are they allowed to print or save any documents to disc. As one of the Cuban dissidents explains: “The high [email-access] prices, which disguise high taxes, are a subtle form of censorship, and they finance everything from new investment to the maintenance of the repressive apparatus.”5
Several nations with wealthier populations allow limited Internet access but block any website that is critical of the government. The only nations (out of those that allow Internet access at all) to have successful website blocking programs at the ISP level are China and Saudi Arabia.2 However, the Internet has over 36 million websites6, and it is impossible to block all the objectionable ones. It is estimated that over 30,000 people in China work on filtering out websites1 and the cost of manual filters and Cisco-developed filtering technology makes the cost of finding every single objectionable site prohibitive. To complicate the problem, supporters of democracy often set up mirrors (exact duplicates) of banned sites abroad, and a number of governmental and non-governmental organizations are working to set up automated methods for creating alternative access routes to blocked sites. This is where Google comes in. Its automated spider crawls the web from link to link and indexes all the sites it finds in a giant database. Google also creates copies, or a cache the sites it finds, so that it can be access when it’s down (or blocked.) Furthermore, Google constantly and automatically updates its indexes, so that each day brings fresh search results from new sites. Because China does not have the resources to index every single site, it apparently decided to block the entire search engine. As a recent Newsweek article put it, “When the Chinese government decided that the Web offered its citizenry an overly intimate view of the world outside its borders, what better way to pull down the shades than to block Google?” By blocking the entire search engine, it tried to make it significantly harder for dissenters to communicate and locate unblocked (and cached) versions of undesirable sites.
However China’s blocking of Google was not entirely successful. Many websites have licensing deals with Google, and blocking them would require blocking most major search engines and many other sites. Hours after Google was blocked, part of Yahoo and AltaVistsa were blocked because media sites immediately reported ways to get around the block. Since then, the ban on most Google-enabled sites has been lifted in lieu of new technology that filters out particular search results (“cache”, the term for Google saved archive of a site is one of them) or simply disconnects the user from the Internet.
In addition to blocking websites on the ISP side, China has attempted to control access from the user’s side as well. Earlier this year, citing “fire hazards” and “students who died of fatigue in cafes,” China shut down thousands of cafes, imposed mandatory filters, a voluntary “Public Pledge on Self-Discipline” and time and age restrictions on café use. Furhermore, a ban on a particular nation’s media outlets seems to travel along with the Dalai Lama.8 With such policies, China hopes to make access to “dangerous” ideas more difficult. It is widely acknowledged that China can never block every single dissident site, but my raising the amount of effort needed to communicate with fellow dissidents at home and abroad, it thinks it can prevent the medium from being used for reasons “harmful to social stability.” 9
The fact that China does not ban Internet access completely is an indicator that that the government does not have a free hand to impose dis-incentives against undesirable activity. While blocking Internet access completely would be a more effective way to prevent coordination, this may also be too costly as solution because of the vital role the Internet plays in integrating China into the world market and China’s desire to enter various international trade organizations. Furthermore, China removed most of the blocks on Google less than a week after they began, probably a response to the combination of negative media coverage and complaints from its own researchers. Overly harsh punishments also have the risk of creating martyrs and arousing public resentment. Thus, authoritarian regimes must maintain a balance between suppressing and punishing expression of undesirable ideas and keeping the resources and attention on their activities to a minimum.
What kind of strategies could dissidents use to overcome government efforts at censorship? The Internet, with its anonymous and encrypted means of communication, provides unique opportunities to circumvent official restrictions. The ability to locate websites on foreign servers is another great advantage to dissidents– it’s hard to operate a printing press or a even server (because IP addresses can be tracked down to their origin) in secret from one’s own government, but moving operations abroad doesn’t raise the cost of communication while preventing raids and confiscation of equipment for the dissidents. (This isn’t always true: China has been the origin of a number of hacking incidents in various universities and government agencies, including several library servers at Texas A&M earlier this year.) Furthermore, the support of governmental and non-governmental projects in democratic countries can be a big help to dissidents, by creating new technologies such as Peekabooty, and Triangle Boy, which may also go a long way towards this goal. These technologies create encrypted networks that have no central point of origin and facilitate anonymous access to shared documents and/or regular websites. The Global Internet Freedom Act, a proposed bill in Congress to create an Office of Global Internet Freedom with a 50 million dollar budget may also be of great help to raising the costs to China of censoring democratic movements. Pressure from major media networks has also been successful in opening access to blocked sites, as widespread condemnation of China’s blocking of western news outlets has led it to reopen access to some of the sites.
Whether immediate efforts to prevent coordination among dissidents are successful, China’s attempts at censorship are bound to fail in the long run. Because the Internet’s value as a commercial and research tool are bound to grow, and are closely intertwined with alternative uses, the costs of preventing access to any particular material is bound to become prohibitively expensive, especially with the rapid and exponential growth of Internet users in China. Meanwhile, the best strategy democratic nations can follow is to make China’s censorship policy as costly as possible by sponsoring the development of circumvention technologies.
References
1 “Replacement of Google with Alternative Search Systems in China”
http://cyber.law.harvard.edu/filtering/china/google-replacements/
2. Felipe Rodriquez. (30 November 2002 ) ‘Freedom of the Media and the Internet’. Paper for the OSCE workshop
http://www.xs4all.nl/%7Efelipe/OSCE_paper.pdf
3. Martha Beatriz Roque Cabello. Every Cuban Has a Built-In Policeman
http://www.cubafacts.com/Commentary/roque1.htm
4. John DeSio. (January 2, 2002) First pro-democracy Web site in Cuba is launched. Digital Freedom Network
http://dfn.org/focus/cuba/roque-website.htm
5. Manuel David Orrio. (October 8, 2001) Independent Cuban journalist gets access to e-mail. Cooperativa de Periodistas Independientes (CPI)
http://dfn.org/focus/cuba/expensive.htm
6. Internet starts to shrink. (January, 2002) BBC Sci/Tech News
http://news.bbc.co.uk/1/hi/sci/tech/1738496.stm
7. Bobson Wong. (July 23, 2002) Chinese Internet clampdown continues after cybercafe fire. Digital Freedom Network
http://www.dfn.org/news/china/cafe-reopen.htm
8. Bobson Wong (April 25, 2002) Temporary Chinese ban on Australian news site ends. Digital Freedom Network
http://www.dfn.org/news/china/abc-ban.htm
9. Zhao Ying, “information and security issues,” Jingji Guanli, no.5, may 5. 1998pp as printed in Rand Report ‘You’ve got dissent!’ pp48 chapter two, government counter strategies
10. Steven Levy. (Dec. 16, 2002) The World According to Google
http://www.msnbc.com/news/844175.asp?0dm=T11PT
11. Paul Wilkinson. (October 2, 2002) Bipartisan, Bicameral Bill Stops Internet Jamming
http://policy.house.gov/html/news_release.cfm?id=111
The anti-war protesters: what are they for?
Dec 7th
I’ve written a new essay: The anti-war protesters: what are they for?
(shorter version:)
“A recent incident at University of Texas is indicative of the nature of the pacifists opposing a war with Iraq. After the student government of the University of Texas passed a resolution condemning a U.S. attack on Iraq, the Young Conservatives attempted a debate with the “Campus Coalition for Peace and Justice.” However, as CNN reported, “Most listeners in the audience seemed to agree with the Campus Coalition, or at least people on that side seemed more vocal about their feelings. When an antiwar advocate began heckling a student in the pro-war camp, other supporters of the President’s policies stood up, and a fistfight almost broke out.” One can easily imagine what “more vocal” means when reverse-translated through the filter of CNN’s liberal bias. Apparently, the “peace protesters” are not so peaceful. All over the world, they have been rioting against “aggression.” What is the true nature of the anti-war sentiment in America then? Much insight about the nature of the “anti-war” protest can be found in their “Statement of Conscience,” which has been endorsed by thousands of professors and students across America.”
The anti-war protesters: what are they for?
Dec 7th
A recent incident at University of Texas is indicative of the nature of the pacifists opposing a war with Iraq. After the student government of the University of Texas passed a resolution condemning a U.S. attack on Iraq, the Young Conservatives attempted to engage them in a debate with the “Campus Coalition for Peace and Justice.” However, as CNN later reported, “Most listeners in the audience seemed to agree with the Campus Coalition, or at least people on that side seemed more vocal about their feelings When an antiwar advocate began heckling a student in the pro-war camp, other supporters of the President’s policies stood up, and a fistfight almost broke out.” One can easily imagine what “more vocal” means when reverse-translated through the filter of CNN’s liberal bias. Apparently, the “peace protesters” are not so peaceful. All over the world, they have been rioting against aggression. What is the true nature of the anti-war sentiment in America then? Much insight about the nature of the “anti-war” protest can be found in their “Statement of Conscience,” which has been endorsed by thousands of professors and students across America.
The Statement begins with seemingly noble remarks: “peoples and nations have the right to determine their own destiny questioning, criticism, and dissent must be valued and protected. such rights and values are always contested and must be fought for.”
It is unclear to me however, who’s “rights” the protesters support . Is it Saddam’s “right” to violently suppress dissent by gassing thousands of his own people, and attacking Iran, Kuwait, and Israel? If the protesters are truly concerned about dissenters, why aren’t they showing any support for the opposition groups that seek to establish a democratic government in Iraq? Do they believe that the bloody coup in which Saddam Hussein became dictator gives him a “right” to do as he pleases with anyone who crosses his path?
The resolution goes on to claim: “Dissident artists, intellectuals, and professors find their views distorted, attacked, and suppressed.” When one considers the behavior of the anti-war protesters in America‘s universities, this statement seems especially misleading. At my own Texas A&M, stands of the “The Examiner,” a local conservative student paper were vandalized and the newspapers stolen by an unknown culprit. It is unclear whether he was offended by the article titled “[Condoleezza] Rice: Iraqis cannot eat their oil reserves” or “Conservative student publications plagued by theft.” In universities like Berkeley, “pro-peace” students have vandalized opposing newspaper offices, and claimed “aggression” when they were arrested for trespassing. Clearly, when supporters of America‘s right to self-defense find their newspapers vandalized and are labeled racists and bigots, it is not they who are suppressing speech.
The most common claims of the antiwar protesters is that Iraq is President Bush’s excuse to promote oil interests and cover up the faltering economy. But is there any truth to either of these claims?
“A Crude View of the Crisis in Iraq,” a Washington Post story, reports that the outcome of regime change in Iraq is far from clear: American companies may be denied access to Iraq as they were in Kuwait, and a new Iraqi government may develop oil production on it’s own, taking a significant time to do so without any major influence on oil prices. On the other hand, it is also likely that Saddam will attempt to destroy as much infrastructure as possible on his way out, so that it will take many years to put out the fires and rebuild Iraq‘s oil production capability. In any case, the effect of a war on American oil interests is far from certain and has not even been brought up in discussion with Iraqi opposition.
The second claim — that Bush is pushing for a war to distract Americans from the economy is equally ridiculous. Liberals who are bitter about the GOP win claim that the Republicans blew the terrorist threat out of proportion to avoid focusing on the economy. However, a recent Gallup poll shows that fully 57 percent of Americans believe that the economy is better off in republican hands and 67 percent believe that the war against terrorism would be better handled by republicans. While I would dispute that either party has handled terrorism or the economy very well, it is clear that most Americans support the Republicans in both of these areas.
The resolution attacks immigration procedures for singling out certain nationalities ignoring the fact that a Saudi national is, oh about 100% more likely to be a terrorist than someone from Sweden or Japan. The peaceniks oppose the racist policy of giving 18 to 40 year old Arab men more scrutiny in airports than a grandma going to see her grandkids while supporting race-based admission policies in universities.
The protesters’ claim that the war on terrorism has given “police sweeping new powers of search and seizure” and “brought down a pall of repression over society.” However, when one considers how vocal the protesters have been in the media, a “pall of repression” is nowhere to be found. On the other hand, when my own “conservative” university banned students from hanging American flags outside their windows, so as “not to offend international students,” the true direction of repression became clear. If indeed the government is holding American citizens without trial or due process, there is cause for concern, but it is only an evasion of the real threat to our security to claim that we should ignore legitimate national interests because of the potential for abuse.
But the protesters’ real agenda has little to do with Iraq. Suppose that after a thorough and unhampered search, the inspectors discover that all those hidden bunkers and presidential palaces are actually full of unanimous ballots from his last election. (Which, according to Saddam, was an 11,445,638 to 0 “Yes” vote.) Suppose that the chemical weapons and arms sales to Iraq that Yugoslavian officials have recently admitted to were actually fireworks for the celebration of Saddam’s election victory. Would I change my mind and oppose going to war with Iraq? Sure.
But suppose that despite Hans Blix’s negotiations with Saddam on the restrictions of our unrestricted access to Iraq, we find evidence of weapons of mass destruction. Will the anti-war protesters change their minds? The answer can be found in their Statement: “What kind of world will this become if the U.S. government has a blank check to drop commandos, assassins, and bombs wherever it wants?” — and this is their reply. Their objection is not so much to Bush’s policy towards Iraq, but in the fact that he may engage in it unilaterally – without the permission of the rest of the world. Robert Jehnsen, author of inspiring articles such as “U.S. just as guilty [as the terrorists] of committing own violent acts” claims to represent the “No-war Collective,” and this is just how he sees the world — as a collective in which the United States must ask for permission to defend itself against terrorism.
The pacifists cannot honestly object to the fact a war may lead to the death of Iraqi civilians — they do not protest the civilians Saddam kills every day. Neither can they complain that “dissent is being silenced” — they have no problem silencing dissent here in America, or to Saddam’s silencing dissent in Iraq. The Statement accuses the government of “putting out a simplistic script of ‘good vs. evil’” — but what the antiwar crowd opposes is any declaration of moral legitimacy in fighting the war on terrorism. They ask “What kind of world will this become if the U.S. government has a blank check to drop commandos, assassins, and bombs wherever it wants?” but they don’t oppose a world where terrorists and dictators have a blank check to the same. Despite their rhetoric, to the peaceniks, there is no difference between a barbaric dictatorship and a free democracy fighting for its very existence (as Israel is) or freedom from terrorism (as the United States is). As their “Statement of Conscience” shows, their primary objection is not that America may go to war with Iraq, but that it may do so unilaterally without the permission of the rest of the world. What the protesters in fact claim, is that any evaluation that a democratic regime is morally superior to a bloody dictatorship is evil, and any difference between the U.S. and Iraq is a probably result of “western imperialism.”
A recent CNN photomontage shows young Palestinian kids with automatic weapons and war-paint on their faces screaming furiously at the camera protesting against a war in Iraq. The next slide shows a protest in America, with an unshaven man in a crowd of angry faces with banners proclaiming “no bombing of children for oil.” Despite the fact that the Palestinians live in an oppressive, violent, and primitive society and the American protesters grew up in the wealthiest, freest, and most successful nation on earth, the differences almost seem lost in the two photos. Perhaps this is what the pacifists are truly after.


Can you spot the difference?
Dec 4th
 View David Veksler’s profile
View David Veksler’s profile
Talkback